Rust Magazine
Issue 2
 / No. ⁨7⁩
translation
edit
用 Egg 实现 SQL 优化器
2023-03-07
avatar wangrunji
#tutorial #database #optimizer

用 Egg 实现 SQL 优化器

SQL 优化器是关系型数据库系统中的重要模块，其作用是对 SQL 语句进行优化，以提高查询效率。为了帮助初学者理解 SQL 优化器的基本原理，我们用 Rust 语言基于 Egg 框架实现了一个小巧的 SQL 优化器。它的代码量不超过一千行，但是涉及表达式化简、常量折叠、谓词下推、列裁剪、连接重排序、代价估计等经典的优化技术，覆盖了基于规则（RBO）和基于代价（CBO）两种优化模式，并且能够在实际的 TPC-H 查询上工作。

本文将简单介绍这个项目的实现过程。你可以在 SQL Optimizer Labs 中找到相关代码，或者在 RisingLight 项目中了解它的实际应用。

GitHub - risinglightdb/sql-optimizer-labs: 🚧 Build a SQL optimizer in 1000 lines of Rust using egg.
🚧 Build a SQL optimizer in 1000 lines of Rust using egg. - GitHub - risinglightdb/sql-optimizer-labs: 🚧 Build a SQL optimizer in 1000 lines of Rust using egg.
https://github.com/risinglightdb/sql-optimizer-labs

Egg 框架

Egg 是一个用 Rust 编写的程序优化器框架。其核心技术基于 Equality Saturation 方法对表达式进行重写和优化。这种方法的思想是通过逐步重写找到表达式的所有等效形式，然后在其中找到最优方案。在此过程中，egg 使用 e-graph 数据结构，能够在运行时高效地查询和维护等价类，从而减少程序优化的时间和空间成本。

GitHub - egraphs-good/egg: egg is a flexible, high-performance e-graph library
egg is a flexible, high-performance e-graph library - GitHub - egraphs-good/egg: egg is a flexible, high-performance e-graph library
https://github.com/egraphs-good/egg

下面这张图来自 egg 官网，从左到右逐步展示了将表达式 a * 2 / 2 优化为 a 的过程。

以其中第二幅图为例，我们可以看到它包含了 e-graph、e-class、e-node 三层结构。

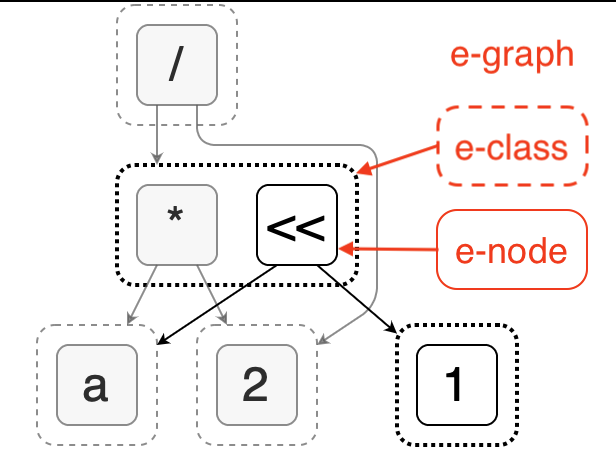
图中每个节点是 e-node，可以表示变量、常量或者操作。多个 e-node 可以组成一个 e-class，代表了一组等价的节点，它们具有相同的语义并且可以互相替换。每个 e-node 的子节点都是 e-class，它们共同组成了 e-graph。因此这种数据结构可以用紧凑的空间表示大量可能的组合方式。

E-graph 还支持动态地插入 e-node 以及合并 e-class，利用这些就可以实现表达式的重写。下图就展示了向图中插入新的表达式 a << 1 ，并与 a * 2 合并等价类的过程。

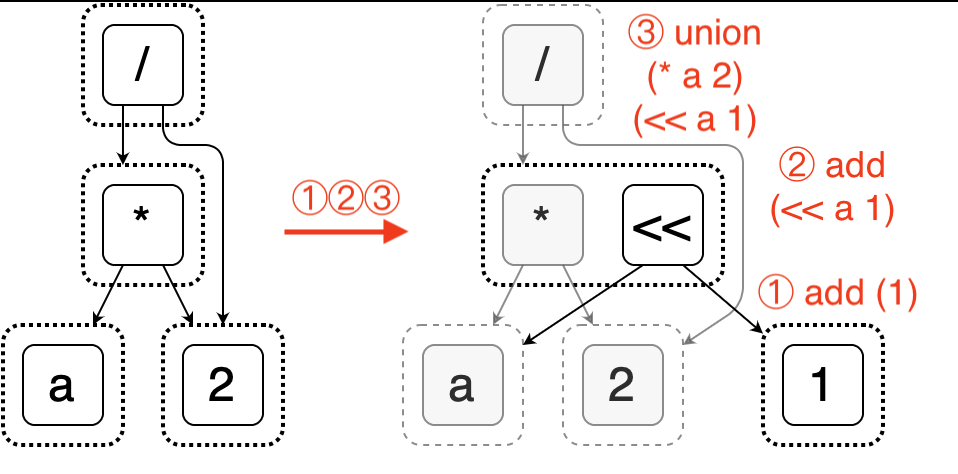
Egg 支持用户使用 Lisp 表达式自定义规则，例如上图的规则可以表示为 (<< ?a 1) => (* ?a 2)。如有需要还可以用 Rust 编写更复杂的规则，这使得它具有高度的灵活性和扩展性。开发者可以基于 egg 快速为自己的语言实现一个优化器。本文接下来就展示了它在 SQL 语言上的应用。

最后值得一提的是，egg 背后的学术论文还获得了 POPL 2021 的杰出论文奖。如果感兴趣，你可以在他们的网站上找到更多相关资料。

定义 SQL 语言

使用 egg 的第一步是定义语言，在本文中就是 SQL 语句和其中的表达式。

egg 充分利用了 Rust 语言中的代数数据类型（ADT）来定义语言。我们可以用它提供的 define_language 宏定义一个 enum 来描述一个节点：

define_language! {
    pub enum Expr {
        // values
        Constant(DataValue),            // null, true, 1, 1.0, "hello", ...
        Column(ColumnRefId),            // $1.2, $2.1, ...

        // list
        "list" = List(Box<[Id]>)        // (list ...)

        // operations
        "+" = Add([Id; 2]),             // (+ a b)
        "and" = And([Id; 2]),           // (and a b)

        // plans
        "scan" = Scan([Id; 2]),         // (scan table [column..])
        "proj" = Proj([Id; 2]),         // (proj [expr..] child)
        "filter" = Filter([Id; 2]),     // (filter condition child)
        "join" = Join([Id; 4]),         // (join type condition left right)
        "hashjoin" = HashJoin([Id; 5]), // (hashjoin type [left_expr..] [right_expr..] left right)
        "agg" = Agg([Id; 3]),           // (agg aggs=[expr..] group_keys=[expr..] child)
        "order" = Order([Id; 2]),       // (order [order_key..] child)
            "asc" = Asc(Id),                // (asc key)
            "desc" = Desc(Id),              // (desc key)
        "limit" = Limit([Id; 3]),       // (limit limit offset child)
    }
}

上面代码是一个简化版本，其中包含了四种节点类型：值，列表，操作符和算子。

  1. 值类型：表达式中的叶子节点。它可以是一个常量 Constant，或者一个变量 Column 引用数据库表中的一列。
  2. 列表：这是我们引入的一种特殊节点，表示若干元素组成的有序列表。它可以有任意多个子节点。注意到从这里开始，每个类型的定义前面都多了一个字符串字面量。它被用来在 Lisp 表达式中标识这个节点。具体的表示方法如右边注释中所示。
  3. 操作符：通常是表达式中间节点。它关联的 Rust 类型可以是 Id，[Id; N]或者 Box<[Id]>，分别表示 1 个，N 个，或不定长个子节点。
  4. 算子：类似于操作符，只不过它作用于一个表而不是一个值。一条 SQL 语句会被转化为由若干算子组成的执行计划树。每个算子中除了子节点（child，left，right）是算子，还会包含若干由表达式组成的参数。

比如说对于这样一条 SQL 语句：

SELECT users.name, count(commits.id)
FROM users, repos, commits
WHERE users.id = commits.user_id
	AND repos.id = commits.repo_id
	AND repos.name = 'RisingLight'
	AND commits.time BETWEEN date '2022-01-01' AND date '2022-12-31'
GROUP BY users.name
HAVING count(commits.id) >= 10
ORDER BY count(commits.id) DESC
LIMIT 10

它的执行计划可以用我们定义的语言表示成这样的形式：

(proj (list $1.2 (count $3.1))
  (limit 10 0
    (order (list (desc (count $3.1)))
      (filter (>= (count $3.1) 10)
        (agg (list (count $3.1)) (list $1.2)
          (filter (and (and (and (= $1.1 $3.2) (= $2.1 $3.3)) (= $2.2 'RisingLight'))
                    (and (>= $3.4 '2022-01-01') (<= $3.4 '2022-12-31')))
            (join inner true
              (join inner true
                (scan $1 (list $1.1 $1.2 $1.3))
                (scan $2 (list $2.1 $2.2 $2.3)))
              (scan $3 (list $3.1 $3.2 $3.3 $3.4 $3.5))
)))))))

我们现在要做的就是定义一系列规则对上述表达式进行等价变换，最终找到一个代价最小的表示作为优化结果。

定义优化规则

在这一节中，我们将利用 egg 提供的 API 来描述优化规则。由于篇幅所限，我们将选择其中具有代表性的几种进行简单介绍。它们分别是：

  • 表达式化简
  • 常量折叠
  • 谓词下推
  • HashJoin
  • 连接重排序
  • 代价函数

表达式化简

首先我们对算子中的表达式进行化简。

比如对一开始提到的乘法转位移规则，在 egg 中可以用 rewrite 宏描述如下：

rewrite!("mul2-to-shl1"; "(* ?a 2)" => "(<< ?a 1)")

=> 两侧的字符串分别表示变换前后的表达式模式，其中 ?a 表示可以替换成任何表达式的变量。当 egg 执行器搜索到符合这个模式的表达式后，会按照右边的模式生成一个新的表达式，并将其和原来的节点 union 起来形成等价类。另外，这里的 => 也可以替换成 <=> 表示双向变换。

对于另一些规则来说，它们还需要附加一定的执行条件。例如下面的化简仅在除数非 0 时才有效：

rewrite!("div-self"; "(/ ?a ?a)" => "1" if is_not_zero("?a"))

这里我们使用了 is_not_zero 函数来判断变量 ?a 是否非 0。不过我们如何才能知道一个表达式是否非 0 呢？这时就需要引入表达式分析。

常量折叠

Egg 的表达式分析功能允许我们为每个等价类关联任意值来描述它的某些特性。例如：它是不是常数，它是什么数据类型，其中引用了哪些列等。比如为了解决上面的问题，我们可以引入常量分析。它会判断每个节点对应的表达式是不是常数，以及具体的常数值。下图展示了上文中表达式的常量分析结果。

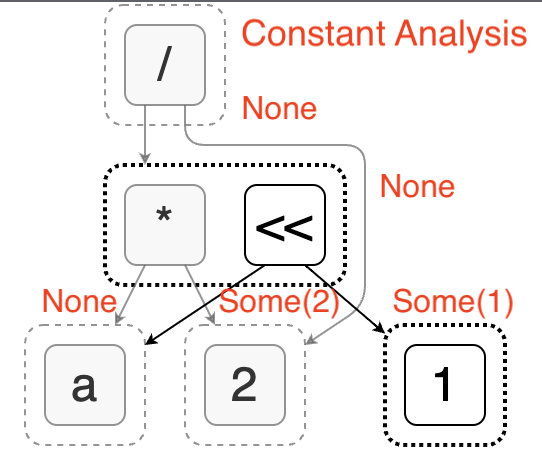
在表达式分析的过程中，egg 还允许我们修改 e-graph，进行节点添加或合并。利用这一机制我们就可以实现常量折叠优化：将确定是常量的表达式替换为单个值。

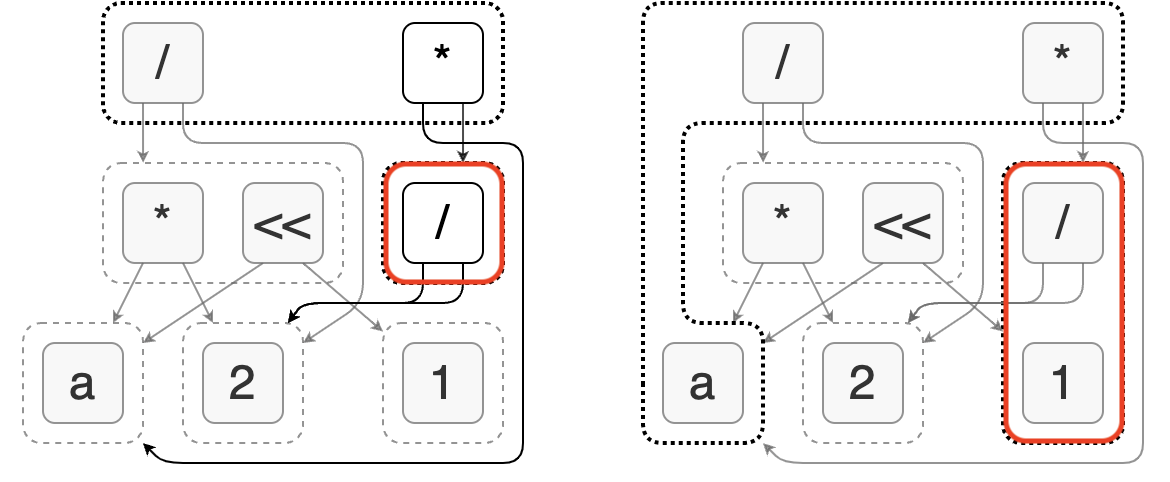
如左图所示，在常量分析中我们发现 (/ 2 2) 节点等价于常数 1。此时我们创建一个新节点 1 （会发现已经存在于图中）并将其与 (/ 2 2) 合并。这样就完成了常量折叠优化。它的特点是利用了表达式分析的副作用，而不是通过重写规则完成的。

落实到代码中，每一种表达式分析都需要实现 Analysis trait。它的文档就以常量折叠为例，介绍了实现表达式分析的具体步骤。感兴趣的读者可以点开了解更多细节。

谓词下推

完成对表达式的化简后，我们来看对 SQL 算子的优化。其中一个经典优化是谓词下推。

谓词下推的思想是将 Filter 算子中的谓词尽量下推到底层算子上，来更早地过滤掉不需要的数据，从而降低上层算子要处理的数据量。例如下图展示了将 Join 上面的 Filter 算子下推到底层的过程。其中主要分为两个步骤：

  1. 将 Join 上面的 Filter 谓词下推到 Join 的连接条件上
  2. 将 Join 的连接条件下推到左右子节点中，生成一个新的 Filter 算子

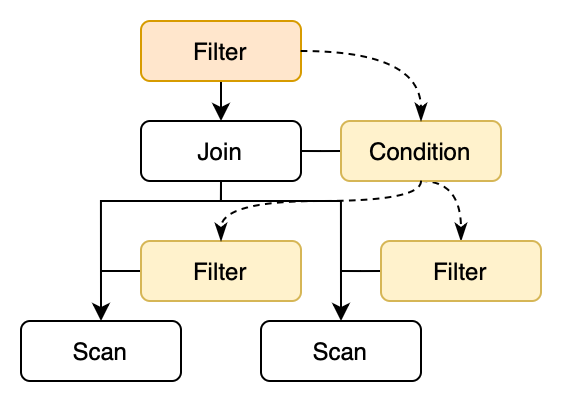
第一步可以用非常简单的规则描述：

rewrite!("pushdown-filter-join";
    "(filter ?cond (join inner ?on ?left ?right))" =>
    "(join inner (and ?on ?cond) ?left ?right)"
)

但是第二步就比较棘手了，因为这里有三种可能情况：

  1. ↙️  谓词只包含来自左侧的列，可以下推到左子树中
  2. ↘️  谓词只包含来自右侧的列，可以下推到右子树中
  3. ⏹️  谓词同时包含左右两边的列，无法下推

此时我们需要继续使用 egg 的条件重写功能。只有当谓词中引用的列满足一定条件时，我们才能把它推下去：

rewrite!("pushdown-filter-join-left";
    "(join inner (and ?cond1 ?cond2) ?left ?right)" =>
    "(join inner ?cond2 (filter ?cond1 ?left) ?right)"
    if columns_is_subset("?cond1", "?left")
),

这里函数 columns_is_subset(a, b) 的语义为：表达式 a 所使用的列的集合，是否包含于算子 b 所提供的列的集合。为此我们需要引入新的表达式分析：Column Analysis，来计算每个节点所使用和定义的列的集合。这有点类似于活跃变量分析中的 use 和 def 集。它的具体实现过程也不复杂，读者可以参考 RisingLight 项目中的代码自行体会。

除了下推 Filter 算子以外，我们还可以下推 Projection 算子，并且在过程中对沿途算子进行列裁剪。列裁剪可以去掉上层算子不需要的列，从而减少扫描和传输开销。

HashJoin

下一个优化是将 Join 算子换成更高效的 Hash Join。Hash Join 的基本思想是：首先对一边的数据建立 Hash 表，然后遍历另一边的数据，在 Hash 表中查找匹配项。它的时间复杂度为 O(N + M)，通常远远优于嵌套循环连接的 O(N * M)。

在 Egg 中实现 Hash Join 优化也非常简单。它的主要功能是识别形如 l1 = r1 AND l2 = r2 AND … 这样的连接条件，然后将左右两边的 key 分开存放到 HashJoin 节点中。这样方便未来执行器直接从左右两边的输入中提取数据。

rewrite!("hash-join-on-one-eq";
    "(join ?type (= ?l1 ?r1) ?left ?right)" =>
    "(hashjoin ?type (list ?l1) (list ?r1) ?left ?right)"
    if columns_is_subset("?l1", "?left")
    if columns_is_subset("?l2", "?right")
),

对于连接条件中包含两个或更多等式的情况，也可以用类似的方式描述。

连接重排序

除了优化连接算法以外，我们还可以调整多个连接的顺序，使得整体的执行代价最小。不同的连接顺序需要的执行开销可能会大相径庭。

对于常用的内连接，它满足交换律和结合律。从执行计划树的角度来看，交换律相当于交换 Join 节点的左右子树，结合律相当于对二叉树进行旋转。

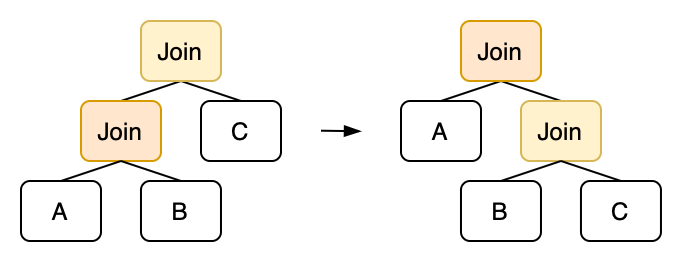
在 egg 中描述结合律也非常直观：

rewrite!("join-right-rotation";
    "(join inner true (join inner true ?left ?mid) ?right)" =>
    "(join inner true ?left (join inner true ?mid ?right))"
),

注意这里我们没有考虑 Join 算子上有条件的情况。因为假如最上层的 Join 算子条件中包含来自 A 的列，那么它就不能被转到右边去。如果考虑条件的话，可能需要借助 Column Analysis 来构造更复杂的规则。

类似的，我们还可以实现交换律：

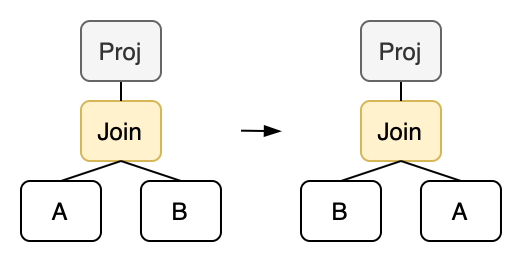
rewrite!("join-swap";
    "(proj ?exprs (join inner ?cond ?left ?right))" =>
    "(proj ?exprs (join inner ?cond ?right ?left))"
),

不过这里我们要求 Join 上面必须有一个 Projection 才能执行交换。因为交换左右子树会导致 Join 算子输出的列发生变化，这不符合我们对等价类的定义。所以我们要在上面套一个 Projection，以保证重写前后两个算子的输出是完全一致的。

使用上述两条规则，我们能够枚举出所有可能的连接顺序。对于 N 个表的连接，就存在着 N! 种不同的排列。在这么多方案中哪个是最优的呢？此时就需要引入代价函数，根据各个表的实际规模进行计算和选择。

代价函数

在前面几个优化中，重写后的表达式一定比之前更优，它们属于基于规则的优化（RBO）。而连接重排序需要引入代价函数评估不同方案，选择开销最小的执行，属于基于代价的优化（CBO）。

由于 Equality Saturation 方法本身就是基于代价的，因此在 egg 中实现 CBO 易如反掌。我们只需在 CostFunction trait 下实现代价函数：

pub struct CostFn<'a> {
    pub egraph: &'a EGraph,
}
impl egg::CostFunction<Expr> for CostFn<'_> {
    type Cost = f32;
    fn cost<C>(&mut self, enode: &Expr, mut costs: C) -> Self::Cost
    where
        C: FnMut(Id) -> Self::Cost,
    {
        use Expr::*;
        // 定义一些辅助函数：
        // rows:  估计算子输出的行数
        // cols:  算子输出的列数
        // out:   输出的数据量 = rows * cols
        // costs: 节点的总代价
        match enode {
            Scan(_) | Values(_) => out(),
            Order([_, c]) => nlogn(rows(c)) + out() + costs(c),
            Proj([exprs, c]) | Filter([exprs, c]) => costs(exprs) * rows(c) + out() + costs(c),
            Agg([exprs, groupby, c]) => (costs(exprs) + costs(groupby)) * rows(c) + out() + costs(c),
            Limit([_, _, c]) => out() + costs(c),
            TopN([_, _, _, c]) => (rows(id) + 1.0).log2() * rows(c) + out() + costs(c),
            Join([_, on, l, r]) => costs(on) * rows(l) * rows(r) + out() + costs(l) + costs(r),
            HashJoin([_, _, _, l, r]) => (rows(l) + 1.0).log2() * (rows(l) + rows(r)) + out() + costs(l) + costs(r),
            Insert([_, _, c]) | CopyTo([_, c]) => rows(c) * cols(c) + costs(c),
            Empty(_) => 0.0,
            // 对于其它表达式，设定代价为 0.1 x AST size
            _ => enode.fold(0.1, |sum, id| sum + costs(&id)),
        }
    }
}

这个函数作为一个示例，主要考虑了算子的计算量和输出的数据规模。在实际开发中可能需要对代价函数进行多次微调，才能让优化器找到相对合理的结果。

定义好代价函数后，就可以交给 egg 让它找出最优的表达式。Egg 提供了 Runner 来自动完成这一过程：

/// 优化给定的执行计划
pub fn optimize(expr: &RecExpr) -> RecExpr {
    // 给定初始表达式和重写规则，进行等价类扩展
    let runner = egg::Runner::default()
        .with_expr(&expr)
        .run(&*rules::ALL_RULES);
    // 给定代价函数，提取出最优表达式
    let cost_fn = CostFn {
        egraph: &runner.egraph,
    };
    let extractor = egg::Extractor::new(&runner.egraph, cost_fn);
    let (_cost, best_expr) = extractor.find_best(runner.roots[0]);
    best_expr
}

不过，egg 的执行器现在还不太智能，它在扩展等价类的过程中并不会依据代价函数进行启发式搜索，而是暴力扩展出所有可能的表示。对于比较复杂的查询（例如 TPC-H 中常见的多表连接）很容易出现组合爆炸的情况。此外，一些特殊的重写规则可以被应用无数次，产生深度嵌套的表达式，更是助长了这种现象。

多轮迭代+分阶段优化。图源 AlphaGo。

为了避免这一问题，我们可以对上述过程手动迭代多次，每轮迭代抽取出一个最优解作为下一轮的输入。从而实现接近启发式搜索的效果。此外，我们还可以手动将规则划分为几类，进行多阶段优化，每个阶段只应用一部分规则。通过这些方法，我们的优化器就可以在 100ms 左右的时间内将常见的 SQL 语句优化到令人满意的程度了。你可以在这里看到 RisingLight 对 TPC-H 查询的优化结果。

总结

在这篇文章中我们介绍了程序优化器框架 egg，并展示了如何使用 egg 快速开发一个 SQL 优化器。

Egg 的核心原理是 Equality Saturation：通过一些规则对表达式进行重写，然后使用代价函数找到最优方案。开发者在使用 egg 时，首先要定义语言，然后使用 Lisp 表达式描述重写规则，最后定义代价函数。剩下的工作都可以交给框架自动完成。

可以说，egg 是一款强大又易用的程序优化框架，非常适合快速实现各种优化器的原型系统。如果你在工作中遇到类似的需求，或者对写一个数据库优化器感兴趣，欢迎尝试使用 egg！

Previous: Demystifying Rust Lifetimes: A Conversation with ChatGPT